![]()
The resolution and performance of an optical microscope can be characterized by a quantity known as the modulation transfer function (MTF), which is a measurement of the microscope's ability to transfer contrast from the specimen to the intermediate image plane at a specific resolution. Computation of the modulation transfer function is a mechanism that is often utilized by optical manufacturers to incorporate resolution and contrast data into a single specification.
![]()
La risoluzione e le prestazioni di un microscopio ottico possono essere caratterizzate da una quantita' conosciuta come modulation transfer function (MTF), che non e' altro che la misura della capacita' del microscopio di trasferire contrasto dal campione al piano di immagine intermedio, per una specifica risoluzione. Il calcolo della funzione di trasferimento di modulazione e' un meccanismo che e' utilizzato spesso da produttori ottici per incorporare dati di risoluzione e di contrasto in una singola specifica.
The modulation transfer function is useful for characterizing not only traditional optical systems, but also photonic systems such as analog and digital video cameras, image intensifiers, and film scanners. This concept is derived from standard conventions utilized in electrical engineering that relate the degree of modulation of an output signal to a function of the signal frequency. In optical microscopy, signal frequency can be equated to a periodicity observed in the specimen, ranging from a metal line grating evaporated onto a microscope slide or repeating structures in a diatom frustule to subcellular particles observed in living tissue culture cells.
The number of spacings per unit interval in a specimen is referred to as the spatial frequency , which is usually expressed in quantitative terms of the periodic spacings (spatial period ) found in the specimen. A common reference unit for spatial frequency is the number of line pairs per millimeter. As an example, a continuous series of black and white line pairs with a spatial period measuring 1 micrometer per pair would repeat 1000 times every millimeter and therefore have a corresponding spatial frequency of 1000 lines per millimeter.
Another important concept is the optical transfer function (OTF), which represents the ratio of image contrast to specimen contrast when plotted as a function of spatial frequency, taking into account the phase shift between positions occupied by the actual and ideal image. In general terms, the optical transfer function can be described as:
OTF = MTF*e^if(f)
in which the imaginary term represents the phase transfer function (PTF), or the change in phase position as a function of spatial frequency. Therefore, the optical transfer function is a spatial frequency-dependent complex variable whose modulus is the modulation transfer function, and whose phase is described by the phase transfer function. If the phase transfer function is linear with frequency, it represents a simple lateral displacement of the image as would be observed with an aberration such as geometric distortion. However, if the phase transfer function is nonlinear, it can adversely affect image quality. In the most dramatic example, a phase shift of 180 degrees produces a reversal of image contrast, where light and dark patterns are inverted.
A perfect optical system would have a modulation transfer function of unity at all spatial frequencies, while simultaneously having a phase transfer factor of zero. In cases where the image produced by the microscope (or other optical system) is sinusoidal and there is no significant phase shift, the modulus of the optical transfer function reverts to the modulation transfer function.
In situations where the specimen is a periodic line grating composed of alternating black and white lines of equal width (square waves), a graph relating the percentage of specimen contrast transferred to the image is known as the contrast transfer function (CTF). Most specimens display a composition of sinusoidally varying intensities having differing spatial frequencies instead of distinct sharp profiles in the form of square waves. In this case, a graph relating output as a fraction of input intensity versus signal (spatial) frequency is analogous to the modulation transfer function. As the spatial frequency approaches very large values, the square wave response resembles that of a sinusoid, yielding graphs of the contrast transfer function and the modulation transfer function that are virtually identical.
The effect of increasing spatial frequency on image contrast in a diffraction-limited optical microscope is illustrated in Figure 1. A periodic line grating consisting of alternating white and black rectangular bars (representing 100 percent contrast) is presented at two spatial frequencies on the left-hand side of the figure. The resulting image produced in the microscope is shown on the right side of each objective, and appears as a sinusoidal intensity that has reduced contrast, which is plotted in the graph below the image in terms of a relative percentage of the object contrast. One hundred percent contrast represents regular white and black repeating bars, while zero percent contrast is manifested by gray bars that blend into a gray background of the same intensity. After the contrast value reaches zero, the image becomes a uniform shade of gray, and remains as such for all higher spatial frequencies.
When the input is a high contrast square wave, such as the periodic grating target illustrated in Figure 1, transfer of contrast is determined by the contrast transfer function. A majority of specimens observed in the microscope, however, do not display such a regular periodicity and consist of "square waves" that are sinusoidal to varying degrees at the sub-micron level. In this case, the modulation transfer function is utilized to calculate transfer of contrast from the specimen to the image produced by the microscope.
Modulation of the output signal, the intensity of light waves forming an image of the specimen, corresponds to the formation of image contrast in microscopy. Therefore, a measurement of the MTF for a particular optical microscope can be obtained from the contrast generated by periodic lines or spacings present in a specimen that result from sinusoidal intensities in the image that vary as a function of spatial frequency. If a specimen having a spatial period of 1 micron (the distance between alternating absorbing and transparent line pairs) is imaged at high numerical aperture (1.40) with a matched objective/condenser pair using immersion oil, the individual line pairs would be clearly resolved in the microscope. The image would not be a faithful reproduction of the line pair pattern, but would instead have a moderate degree of contrast between the dark and light bars (Figure 1). Decreasing the distance between the line pairs to a spatial period of 0.5 microns (spatial frequency equal to 2000 lines per millimeter) would further reduce contrast in the final image, but increasing the spatial period to 2 microns (spatial frequency equal to 500 lines per millimeter) would produce a corresponding increase in image contrast.
La modulation transfer function e' utile per caratterizzare non solo sistemi ottici convenzionali, ma anche sistemi fotonici proprio come videocamere analogiche e digitali, amplificatori di luce e scanner di pellicole. Questo concetto e' derivato dalle convenzioni standard usate nella ingegneria elettrica, che legano il grado di modulazione di un segnale in uscita, alla funzione della frequenza del segnale. Nella microscopia ottica, la frequenza del segnale puo' essere equiparata ad una periodicita' osservata nel campione. Periodicita' che puo' essere quella di del reticolo di una linea di metallo fatta evaporare su una diapositiva per microscopio o della ripetizione di strutture nel frustolo di una diatomea, o delle particelle subcellulari osservate in cellule viventi di una coltura di tessuto.
Il numero delle spaziature per unita' di intervallo in un campione e' chiamato frequenza spaziale, solitamente espressa in termini di periodo spaziale trovato nel campione. Una comune unita' di riferimento per la frequenza spaziale e' il numero di coppie di righe per millimetro. Per esempio, un serie continua di coppie bianche e nere con un periodo spaziale di 1 micrometro per coppia si ripetera' 1000 volte al millimetro e avra' quindi una frequenza spaziale di 1000 linee per millimetro.
Un altro importante concetto e' quello di optical transfer function (OTF), che rappresenta il rapporto tra il contrasto dell'immagine e quello del campione quando e' graficato in funzione della frequenza spaziale, tenendo conto della differenza di fase tra le posizioni occupate dalla immagine effettiva e quella ideale. In generale, la OTF puo' essere descritta come
OTF = MTF*e^if(f)
in cui la parte immaginaria rappresenta la phase transfer function (PTF) o il cambiamento della posizione di fase in funzione della frequenza spaziale. Quindi, la optical transfer function e' una variabile spaziale complessa, dipendente dalla frequenza il cui modulo e' la modulation transfer function e la cui fase e' descritta dalla phase transfer function. Se la funzione di trasferimento e' lineare con la frequenza, essa rappresenta semplicemente uno spostamento laterale della immagine come se fosse osservata con un'aberrazione, piuttosto che con una distorsione geometrica.. Tuttavia, se la funzione di trasferimento in fase non e' lineare, si possono avere effetti negativi sulla qualita' dell'immagine. Nell'esempio piu' drammatico possibile, una frase shiftata di 180 gradi produce una inversione del contrasto della immagine, dove patterns chiari e scuri risultano invertiti.
Un sistema ottico perfetto dovrebbe avere la MTF di una unita' per tutte le frequenze spaziali e contemporaneamente la PTF uguale a zero. Nei casi in cui l'immagine prodotta dal microscopio ( o da altri sistemi ottici) e' sinusoidale e non c'e' uno sfasamento significativo, il modulo della OTF e' uguale alla MTF.
In situazioni in cui il campione produce un reticolo composto da linee chiare e scure di uguale larghezza (onde quadre), il grafico che riporta la percentuale di contrasto trasferito dal campione all'immagine e' conosciuto come contrast transfer function (CTF). Piuttosto che i profili netti e distinti delle onde quadre, molti campioni mostrano composizioni di intensita' che variano in maniera sinusoidale e che differiscono tra loro nelle frequenze spaziali. In questo caso, il grafico che riporta l'output come la frazione tra l'intensita' del segnale in entrata e la frequenza spaziale del segnale stesso, e' anologo all' modulation transfer function. Quando la frequenza spaziale si avvicina a valori molto elevati, la risposta dell' onda quadra somiglia a quella di una sinusoide, producendo grafici della contrast transfer function e della modulation transfer function che sono virtualmente identici.
L'effetto di una crescente frequenza spaziale sul contrasto di un' immagine per un microscopio ottico a diffrazione limitata, e' illustrato nella figura 1. Il reticolo periodico di linee consiste di un'alternanza di barre rettangolari bianche e nere (che rappresentano il 100 per cento di contrasto) ed e' mostrato, per due differenti frequenze spaziali, nel lato sinistro della figura. L'immagine prodotta dal microscopio e' invece mostrata a destra di ogni obiettivo e appare, in termini di percentuale relativa al contrasto dell'oggetto, con una intensita' sinusoidale che ha ridotto il contrasto riportato nel grafico sottostante. Il cento per cento di contrasto rappresenta la ripetizione regolare di linee bianche e nere, mentre un contrasto dello zero per cento rappresenta linee grigie che si confondono con lo sfondo grigio della stessa intensita'. Quando il contrasto raggiunge lo zero, l'immagine diventa di una unico tono di grigio e rimane di questo tono per tutte le piu' alte frequenze spaziali.
Quando l'imput ha un' onda quadra di elevato contrasto, proprio come il periodic grating target illustrato nella Fig.1,il trasferimento del contrasto e' rappresentato dalla Contrast Transfer Function. La maggior parte dei campioni osservati al microscopio, tuttavia, non mostra questa regolare periodicita' e consiste di "onde quadre" che a livelli di frazioni di micron, sono composte di onde sinusoidali. In questo caso, per calcolare il trasferimento del contrasto dal campione all'immagine prodotta dal microscopio e' utilizzata la modulation transfer function.
La modulazione del segnale in uscita, l'intensita' delle onde di luce che si formano nella immagine del campione, corrisponde alla formazione dell'immagine del contrasto nel microscopio. Inoltre, una misura della MTF per un particolare microscopio ottico, puo' essere ottenuta dal contrasto generato da linee periodiche o da spaziature presenti in un campione, ottenute da intensita' sinusoidali nell' immagine e dipendenti dalla frequenza spaziale. Se il campione, con un periodo spaziale di 1 micron (la distanza tre l'alternanza di linee di assorbimento e di trasmissione in una coppia), e' ripreso con un'alta apertura numerica (1.40) con una coppia obiettivo/condensatore ad immersione d'olio, la singola coppia di linee sara' risolta chiaramente dal microscopio. L'immagine non sara' la fedele riproduzione delle coppie di linee, ma avra' un moderato grado di contrasto tra linee chiare e linee scure (figura 1). Diminuendo la distanza tra le coppie di linee di un periodo spaziale pari a 0.5 micron ( frequenza spaziale pari a 2000 linee per millimetro) il contrasto nella immagine finale sara' ridotto ulteriormente, ma aumentando il periodo spaziale di 2 micron (frequenza spaziale pari a 500 linee per millimetro) si produrra' una corrispondente crescita del contrasto nella immagine.
The limit of resolution with an optical microscope is reached when the spatial frequency approaches 5000 lines per millimeter (spatial period equal to 0.2 microns), using an illumination wavelength of 500 nanometers at high numerical aperture (1.4). At this point, contrast would be barely detectable and the image would appear a neutral shade of gray. In real specimens, the amount of contrast observed in a microscope depends upon the size, brightness, and color of the image, but the human eye ceases to detect periodicity at contrast levels below about three to five percent for closely spaced stripes and may not reach the 0.2-micron limit of resolution.
When a specimen is observed in an optical microscope, the resulting image will be somewhat degraded due to aberrations and diffraction phenomena, in addition to minute assembly and alignment errors in the optics. In the image, bright highlights will not appear as bright as they do in the specimen, and dark or shadowed areas will not be as black as those observed in the original patterns. The specimen contrast or modulation can be defined as:
Modulation (M) = (I(max) - I(min))/(I(max) + I(min))
where I(max) is the maximum intensity displayed by a repeating structure and I(min) is the minimum intensity found in the same specimen. By convention, the modulation transfer function is normalized to unity at zero spatial frequency. Modulation is typically less in the image than in the specimen and there is often a slight phase displacement of the image relative to the specimen. By comparing several specimens having differing spatial frequencies, it can be determined that both image modulation and phase shifts will vary as a function of spatial frequency. By definition, the modulation transfer function (MTF) is described by the equation :
MTF = Image Modulation/Object Modulation
This quantity, as discussed above, is an expression of the contrast alteration observed in the image of a sinusoidal object as a function of spatial frequency. In addition, there is a position or phase shift of the sinusoid that is dependent upon spatial frequency in both the horizontal and vertical coordinates. A good example occurs in video microscopy where the raster scanning process produces slightly different responses resulting in a variation between the horizontal and vertical modulation transfer functions.
The phase response from an ideal imaging system demonstrates a linear dependence on spatial frequency, with a position shift that is independent of the frequency and normalized to zero at zero spatial frequency. In the ideal system, all sinusoidal image components are displaced by the same amount, resulting in a net position shift for the image without degradation of image quality. When the phase response deviates from ideal linear behaviour, then some components will be shifted to a greater degree than others resulting in image degradation. This is especially critical in electronic video systems, which often possess less than ideal phase characteristics that can lead to noticeable loss of image quality. Fortunately, an ideal aberration-free optical system having a circular aperture and a centered optical axis (such as a high-performance microscope) will produce a phase transfer function that has a value of zero for all spatial frequencies in all directions. In this case, phase shifts occur exclusively for off-axis rays and only the modulation transfer function need be considered.
Il limite della risoluzione con un microscopio ottico e' raggiunto quando la frequenza spaziale si avvicina a 5000 linee per millimetro (periodo spaziale pari a 0.2 micron), usando una illuminazione di 500 nanometri ad alta apertura numerica (1.4). A questo punto, il contrasto sara' visibile a stento e l'immagine apparira' come un neutro tono di grigio. Nei campioni reali, la quantita' di contrasto osservato in un microscopio dipende dalla dimensione, illuminazione e colore della immagine, ma l'occhio umano smette di distinguere la periodicita' a livelli di contrasto minori del tre o cinque per cento per linee poco spaziate e non raggiunge la risuluzione limite di 0.2 micron.
Quando un campione e' osservato con un microscopio ottico, l'immagine prodotta sara' abbastanza danneggiata dai fenomeni di aberrazione e diffrazione, oltre che dai difetti di costruzione microscopici e dagli errori di allineamento nell'ottica. Nell' immagine, i punti piu' luminosi non appariranno cosi' intensi come nel campione , e le aree scure o ombreggiate non saranno cosi' scure come si osserva nel pattern originale. Il contrasto del campione o la modulazione puo' essere definita come :
Modulation (M) = (I(max) - I(min))/(I(max) + I(min))
dove I(max) e' il massimo della intensita' raggiunta dal ripetersi della struttura e I(min) e' la intensita' minima trovata nel campione stesso. Per convenzione, la modulation transfer function e' normalizzata ad uno per una frequenza spaziale pari a zero. La modulazione e' tipicamente minore nella immagine che nel campione e spesso si presenta un leggero spostamento di fase nell' immagine relativa al campione. Confrontando numerosi campioni differenti fra loro in frequenza spaziale, ci si accorgera' che sia la modulazione dell' immagine che lo sfasamento, varieranno in funzione della frequenza spaziale. Per definizione, la modulation transfer function (MTF) e' descritta dalla seguente equazione:
MTF = Image Modulation/Object Modulation
questa quantita', come gia' detto in precedenza, e' l'espressione dell' alterazione del contrasto osservato nell' immagine di un oggetto sinusoidale, in funzione della frequenza spaziale. Inoltre, si ha lo sfasamento della sinusoide che dipende dalla frequenza spaziale sia nella coordinata orizzontale che in quella verticale. Un buon esempio e' il caso della video microscopia dove il processo di scansione raster produce risposte lievemente differenti dovute alla variazione tra la modulation transfer function orizzontale e quella verticale.
La risposta in fase di un sistema di imaging ideale risulta linearmente dipendente dalla frequenza spaziale, con uno spostamento di posizione che e' indipendente dalla frequenza ed e' normalizzata a zero ad una frequenza spaziale pari a zero. In un sistema ideale, tutte le componenti sinusoidali dell' immagine sono spostate della stessa quantita', producendo un netto spostamento di tutta l' immagine senza danni per la qualita' della stessa. Quando la risposta in fase si discosta dal comportamento lineare, allora alcune componenti saranno spostate di vari gradi in piu' rispetto alle altre, degradando la qualita' della immagine. Questo fenomeno e' particolarmente critico nei sistemi video elettronici, che spesso possiedono caratteristiche di fase non ideali e possono condurre ad una perdita notevole in qualita' della immagine. Fortunatamente, un sistema ottico ideale, libero quindi da aberrazioni ottiche, avente una apertura circolare e centrata sull'asse ottico (proprio come i microscopi high-performance), produrra' una phase transfer function che ha valore zero per tutte le frequenze spaziali in tutte le direzioni. In questo caso, lo spostamento di fase si presenta esclusivamente per raggi off-axis e bisognera' considerare solo la modulation transfer function.
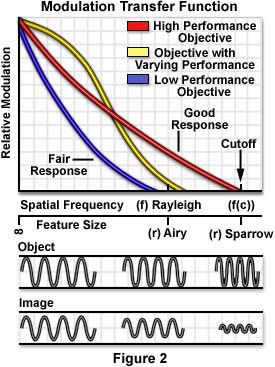
A perfect aberration-free optical system is termed diffraction limited , because the effects of light diffraction at the pupils limit the spatial frequency response and establish the limits of resolution. Presented in Figure 2 is a graph relating the modulation transfer function of a repeating specimen imaged with incoherent illumination by visible light with several different diffraction-limited microscope objectives having a circular pupil. In this case, objective quality affects the modulation response as a function of spatial frequency. Higher quality objectives (red line in Figure 2) exhibit greater performance than those of a lower quality (yellow line), and are able to transfer contrast more effectively at higher spatial frequencies. The objective represented by the yellow curve has the highest performance at low spatial frequencies, but falls short of the high numerical aperture objective at larger frequencies. Beneath the graph is a representation of relative feature size versus spatial frequency with respect to the Rayleigh criteria and Sparrow limit. Also presented is a series of sine waves representing a specimen (object) and the resulting image produced in a typical microscope as the frequency of the sinusoid increases.
When there are no significant aberrations present in an optical system, the modulation transfer function is related to the size of the diffraction pattern, which is a function of the system numerical aperture and wavelength of illumination. In quantitative terms, the modulation transfer function for an optical system with a uniformly illuminated circular aperture can be expressed as:
MTF = 2(f - cos(f) * sin(f)) / p
where
f = acos(ln / 2 * NA)
In these equations, n is the frequency in cycles per millimeter, l is the wavelength of illumination, and NA is the numerical aperture. At low spatial frequencies, image contrast is the highest, but falls to zero as the spatial frequency is increased beyond a certain point (drawn in Figure 2 as a reduction in amplitude produced in the image). The cutoff (f(c)) is the spatial frequency at which contrast reaches zero and can be expressed by the equation :
f(c) = 2 * NA / l
It is interesting to note that this equation expresses (in terms of spatial frequency) the fact that resolution increases with both numerical aperture and shorter wavelengths.
The modulation transfer function is also related to the point spread function, which is the image of a point source of light (commonly referred as the Airy disk) from the specimen projected by the microscope objective onto the intermediate image plane. Optical aberrations and numerical aperture variations affect the distribution of light intensity observed at the image plane, and thus influence the shape of the point spread function. Also note that the sum of the point spread functions produced by a specimen in a diffraction-limited microscope comprises the diffraction pattern produced at the image plane.
Un sistema ottico perfetto, libero da aberrazioni, e' chiamato diffraction limited, perche' gli effetti della diffrazione sulle pupille limita la risposta della frequenza spaziale e stabilisce i limiti della risoluzione. In figura 2 si puo' osservare il grafico del modulation transfer function di un campione periodico ripreso con una illuminazione incoerente di luce visibile con numerosi microscopi diffraction-limited con obiettivi a pupilla circolare. In questo caso, la qualita' dell'obiettivo ha effetti sulla risposta di modulazione in funzione della frequenza spaziale. Obiettivi di alta qualita' (linea rossa in figura 2) lavorano con un maggiore rendimento rispetto a quelli di bassa qualita' (linea gialla) e sono in grado di trasferire contrasto piu' efficientemente a frequenze spaziali piu' alte. L'obiettivo rappresentato dalla curva gialla ha le piu' alte prestazioni a basse frequenze spaziali, ma non riesce ad arrivare ad una alta apertura numerica dell'obiettivo, ad alte frequenze. Sotto il grafico e' riportata la rappresentazione della carattestica grandezza in funzione della frequenza spaziale in accordo con i criteri di Rayleigh e il limite di Sparrow. E'' presentata anche una serie di onde sinusoidali che rappresentano il campione (oggetto) e l' immagine prodotta in un tipico microscopio quando la frequenza della sinusoide cresce.
Quando non ci sono aberrazioni significative presenti in un sistema ottico, la modulation transfer function e' legata alla dimensione del pattern di diffrazione, che e' una funzione della apertura numerica del sistema e della lunghezza d'onda della luce di illuminazione.In termini quantitativi, la modulation transfer function per un sistema ottico con una apertura circolare uniformemente illuminata, puo' essere espressa come:
MTF = 2 * (f - cos(f) * sin(f)) / p
dove
f = acos(ln / 2 * NA)
In queste equazioni, n e' la frequenza in cicli per millimetro, le' la lunghezza d'onda dell' illuminazione, e NA e' l'apertura numerica. A basse frequenze spaziali, il contrasto della immagine e' il piu' alto, ma scende a zero con l'aumentare della frequenza spaziale oltre un certo punto (riportato in figura 2 come riduzione in ampiezza prodotta sull' immagine). Il cutoff (f(c)) e' la frequenza spaziale alla quale il contrasto raggiunge lo zero e puo' essere espressa dall' equazione:
f(c) = 2 * NA / l
E' interessante notare che questa equazione esprime (in temini di frequenza spaziale) il fatto che la risoluzione cresce sia con la apertura numerica che con lunghezze d'onda sempre piu' corte.
La modulation transfer function e' legata inoltre alla Point Spread Function (PSF) che e' l'immagine di una sorgente di luce puntiforme (comunemente riportata come disco di Airy) proiettata da una campione all'obiettivo del microscopio nel piano dell'immagine intermedio.Le aberrazioni ottiche e le variazioni dell'apertura numerica influenzano l'intensita' della distribuzione di luce osservata sul piano dell'immagine, e quindi influenza la forma della point spread function. Si noti, inoltre , che la somma delle point spred function prodotte da un campione in un microscopio diffraction-limited, comprime il pattern di diffrazione prodotto sul piano della immagine.
The highest spatial frequencies that can be imaged by a microscope objective are proportional to the numerical aperture and are based on the distribution size of the point spread function. Objectives with low numerical apertures produce point spread functions that have a wider intensity distribution at the image plane than those formed by objectives with higher numerical apertures. At the limit of resolution, adjacent Airy disks or point spread functions start to overlap, obscuring the ability to distinguish between individual intensities. Narrower intensity distributions (at higher numerical apertures) can approach each other more closely and still be resolved by the microscope. This implies that a narrow point spread function corresponds to a high spatial frequency. In fact, the optical transfer function, a measure of spatial frequency response for an optical system, is the mathematical Fourier transform of the point spread function.
The relationship between the modulation transfer function and the point spread function for a diffraction-limited optical microscope is illustrated in Figure 3. As discussed above, the limiting cutoff frequency (f(c) ) of the modulation transfer function is directly proportional to the objective numerical aperture and inversely proportional to the illumination wavelength. The radius of the first dark concentric ring surrounding the central intensity peak of a point spread function (or Airy disk) is expressed by the equation :
r = 0.61 * l / NA
which is more commonly referred to as the Rayleigh criterion, or the resolution limit of the microscope. Because r is inversely proportional to numerical aperture and directly proportional to the illuminating wavelength, it follows that r and f(c) are also inversely proportional, a fundamental property of Fourier transforms (the width of a function is inversely proportional to the width of its transform).
Le piu' alte frequenze spaziali che possono essere riprese dall'obiettivo di un microscopio sono proporzionali alla apertura numerica e sono basate sulla grandezza di distribuzione della point spread function. Gli obiettivi con una bassa apertura numerica producono point spread function che hanno una distribuzione di intensita' piu' larga sul piano della immagine rispetto a quella formata da obiettivi con aperture numeriche piu' alte. Al limite della risoluzione, gli anelli del disco di Airy adiacenti tra loro e le Point Spread Function iniziano a sovrapporsi, diminuendo la capacita' di distinguere le singole intensita'. Distribuzioni di intensita' piu' strette (a maggiori aperture numeriche) possono avvicinarsi di piu' tra loro e essere risolte comunque dal microscopio. Questo implica che strette point spread function corrispondono ad una alta frequenza spaziale. Infatti, la Optical Transfer Function, una misura della risposta in frequenza spaziale per un sistema ottico, non e' altro che la trasformata di Fourier della Point Spread Function.
La relazione tra la Modulation Transfer e la Point Spread Function per un microscopio ottico a diffrazione limitata e' illustrata nella figura 3. Come gia' discusso, la frequenza di taglio f(c) che limita lamodulation transfer function, e' direttamente proporzionale all' apertura numerica dell'obiettivo e inversamente proporzionale alla lunghezza d'onda della illuminazione. Il raggio del primo anello concentrico scuro che circonda l' intensita' del picco centrale della poin spread function (per un disco di Airy) e' espresso dalla equazione:
r = 0.61 * l / NA
che e' piu' comunemente conosciuto come criterio di Rayleigh o come la risoluzione limite del microscopio. Poiche' r e' inversamente proporzionale all' apertura numerica e direttamente proporzionale alla lunghezza d'onda della illuminazione, segue che r e f(c) sono inversamente proporzionali tra loro, che e' una fondamentale proprieta' della trasformata di Fourier (la larghezza di una funzione e' inversamente proporzionale alla larghezza della sua trasformata).
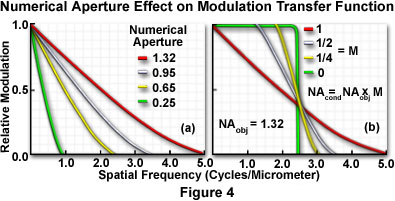
Individual objectives in a microscope display a specific modulation transfer function (or optical transfer function) that depends on numerical aperture, objective design, illumination wavelength, and the mode of contrast generation. When the numerical aperture of the condenser is equal to or greater than that of the objective, the spatial frequency cutoff value decreases with decreasing objective numerical aperture (Figure 4(a)). Holding the objective numerical aperture value constant and varying the condenser numerical aperture results in progressively lower cutoff values with decreasing condenser numerical aperture (Figure 4(b)).
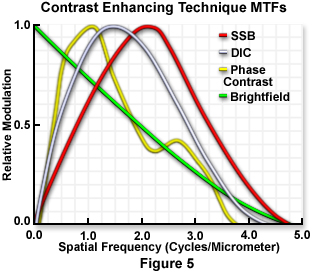
Utilization of contrast enhancing techniques such as phase contrast and differential interference contrast (DIC) results in unique modulation transfer functions that display curves markedly different from those observed in brightfield illumination using the objective's full numerical aperture (Figure 5). For example, the narrow illumination produced by phase rings in phase contrast microscopy produces a modulation transfer function curve that oscillates above and below the brightfield curve, while the curves generated by DIC objectives vary with the angle between the specimen period and the shear direction of the Wollaston or Nomarski prisms. Also illustrated in Figure 5 is the curve produced by a single-sideband edge enhancement microscope (developed by Dr. Gordon W. Ellis), which yields images of superior contrast at high spatial frequencies.
In practice, the performance of a microscope objective or other lens system is often determined by tracing a large number of light rays emitted by a point source in a uniformly distributed array over the vignetted entrance pupil of the objective. After passing through the exit pupil and being distributed over the image plane, the ray intersections are used to plot a spot diagram of the light points at the image plane. In most cases, several hundred rays are utilized to construct a spot diagram, which may take into account optical aberrations if the spacings of light rays are so adjusted. The resulting spot diagram is then regarded as a point spread function and is converted into a graph of the modulation transfer function versus spatial frequency by means of a Fourier transform.
Direct measurements of the modulation transfer function are conducted by utilizing specific test pattern targets consisting of high-contrast periodic line gratings having a series of spacings that usually range from one or several millimeters down to 0.1 micrometer, as illustrated in Figure 8. These targets allow evaluation of microscope objective diffraction patterns, both in and out of focus, in a variety of contrast enhancing modes. Detector arrays are utilized to measure the distribution of light in the image plane by summation of the point spread functions, and a Fourier transform algorithm applied to the data to determine the modulation transfer function.
Ogni obiettivo di un microscopio, preso singolarmente , ha una specifica Modulation Transfer Function (o una Optical Transfer Function) che dipende dall' apertura numerica, dalla struttura dell'obiettivo, dalla lunghezza d'onda della illuminazione e dalla modalita' di generazione del contrasto. Quando l' apertura numerica del condensatore e' maggiore o uguale rispetto a quella dell'obiettivo, il valore della frequenza spaziale di taglio decresce con il decrescere dell' apertura numerica dell'obiettivo. (figura 4(a)). Tenendo costante l' apertura numerica dell'obiettivo e variando invece l'apertura numerica del condensatore si ottengono progressivamente valori decrescenti della frequenza di taglio con il decrescere dell' apertura numerica del condensatore. (figura 4(b)).
L'uso delle tecniche di miglioramento del contrasto, come quella del contrasto in fase e del contrasto dell' interferenza differenziale (DIC), produce un unica MTF che mostra curve marcatamente diverse da quelle osservate per i campi luminosi usando la piu' alta apertura numerica dell' obiettivo (figure 5). Per esempio, la stretta illuminazione prodotta dagli anelli di fase nella microscopia a contrasto di fase, produce una modulation transfer function che oscilla sopra e sotto la curva del campo di illuminazione, dato che le curve generate da obiettivi DIC variano con l'angolo tra il periodo del campione e la direzione di taglio dei prismi di Wollaston o Normaski. In figura 5 e' mostrata anche la curva prodotta da un microscopio di miglioramento di bordo single-sideband (sviluppato dal Dott Gordon W. Ellis), che produce immagini di contrasto superiore, ad alte frequenze spaziali.
In pratica, le prestazioni di un obiettivo per microscopio o di altri sistemi di lenti e' spesso determinata tracciando un grande numero di raggi di luce emessi da una sorgente puntiforme in un insieme uniformemente distribuito sull' entrata vignettata della pupilla dell'obiettivo. Dopo il passaggio dei raggi attraverso l'uscita della pupilla e la distribuzione degli stessi sul piano dell' immagine, le intersezioni dei raggi sono usate per graficare uno spot diagram dei punti di luce del piano stesso. In molti casi, per costruire il diagramma dello spot sono utilizzate molte centinaia di raggi. Il diagramma deve infatti tener conto delle aberrazioni ottiche nel caso in cui le spaziature dei raggi di luce siano cosi' adattati. Il diagramma dello spot cosi' ottenuto e' quindi riportato come una point spead function ed e' convertito in un grafico della modulation transfer function in funzione della frequenza spaziale attraverso la trasfomata di Fourier.
Le misure dirette della modulation transfer function sono condotte utilizzando specifici test pattern target che consistono di reticoli di linee periodiche fortemente contrastate con una serie di spaziature che vanno da un millimetro a frazioni di millimetro fino a 0.1 micrometri, come illustrato in figura 8. Questi targets consentono la valutazione del pattern di diffrazione dell'obiettivo sia in fuoco che fuori fuoco, in una varieta' di modalita' di miglioramento del contrasto. Per misurare la distribuzione della luce nel piano dell' immagine sono utilizzati insiemi di detector, sommando poi le point spred function e applicando successivamente l'algoritmo della trasformata di Fourier ai dati, si determina la modulation transfer function.
The target presented in Figure 6(a) is designed specifically for testing the horizontal modulation transfer function of a macro imaging system such as a telescope, binoculars, video system, camera, or digital video recorder. It is composed of sinusoidal patterns having a spatial frequency range between 0.2 and 80 line pairs per millimeter with a grayscale optical density range varying between 0.2 and 1.2 and an 80 percent modulation of the sine waves. This type of target relays image quality information over a wide range of frequencies and contains on-target references for denoting the contrast levels of the sinusoidal frequencies. In video microscopy, microscopic test targets of sinusoidal targets are not readily available, so the contrast transfer function of a video detector coupled to the microscope is often determined rather than the modulation transfer function.
In systems that have a circular aperture (such as an optical microscope), the modulation and/or contrast transfer function is often computed or measured with star and bar targets similar to the one illustrated in Figure 6(b). Targets of this type have both radial and tangential patterns that are orthogonal to each other and are also useful for detecting focus errors and aberrations such as astigmatism. Variations of the basic star target design contain paired lines and dots that allow determination of objective diffraction patterns both in and out of focus and are useful for measurements conducted in brightfield, reflection contrast, or epifluorescence illumination modes. The wedge and bar spacing period ranges from 0.1 micrometer to tens of microns with spatial frequencies between 0.2 and 25 line pairs per millimeter. Radial modulation transfer targets are ideal for high-resolution measurements using photographic film or analog sensors, but the horizontal and vertical pixelated nature of CCD detectors benefits from analysis utilizing targets that are geometrically consistent with the pixel rows and columns of the imaging device.
Il target mostrato in figura 6(a) e' disegnato specificamente per testare la modulation transfer function orizzontale di un sistema macro di imaging proprio come i telescopi, i binocoli, i video sistemi, le macchine fotografiche o i video recorder digitali. Esso e' composto di un pattern sinusoidale con un range di frequenza spaziale tra 0.2 e 80 coppie di linee per millimetro, con una densita' della scala di grigio che varia tra 0.2 e 1.2 e l' 80% di modulazione delle onde sinusoidali. Questo tipo di target fornisce informazioni sulla qualita' della immagine su un largo range di frequenze e contiene i riferimenti on-target per l'indicazione dei livelli di contrasto delle frequenze sinusoidali. Nella microscopia video, il test target microscopico, non e' consigliabile, per questo motivo e' preferibile determinare la contrast transfer function di un video detector accoppiato ad un microscopio, piuttosto che la modulation transfer function.
Per sistemi che hanno una apertura circolare (come un microscopio ottico), la madulation e/o contrast transfer function e' spesso calcolata o misurata con target a stella o a barre come illustrato nella figura 6(b). Target di questo tipo hanno il pattern radiale e tangenziale ortogonali tra loro e sono utili per rivelare anche errori di messa a fuoco e aberrazioni come l'astigmatismo. Variazioni del disegno di base del target a stella contengono coppie di linee e punti che consentono di determinare il pattern di diffrazione dell'obiettivo sia a fuoco che fuori fuoco e sono utili per le misure condotte su un campo luminoso, per il contrasto per riflessione, o per modi di illuminazione a epifluorescenza. I periodi delle spaziature delle rientranze o delle barre vanno da 0.1 micrometri a decine di micron con una frequenza spaziale tra 0.2 e 25 coppie di linee per millimetro. I modulation transfer target radiali sono ideali per misure ad alta risoluzione in cui si usano pellicole fotografiche o sensori analoghi, ma per la natura orizzontale e verticale della disposizione dei pixel nei sensori CCD, e' meglio usare per l'analisi, target che siano geometricamente consistenti con le righe e le colonne di pixel del dispositivo.
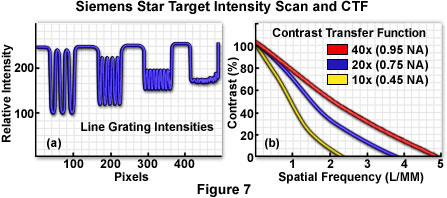
A typical intensity scan made from a star target measured with a high numerical aperture apochromatic objective operating in transmitted light mode is presented in Figure 7(a). Intensity values were averaged over the dimension parallel to the target grating lines. When these types of data are collected for a variety of objectives at varying numerical aperture and plotted as percent contrast versus spatial frequency, a graph similar to that illustrated in Figure 7(b) is obtained. Contrast transfer approaches 100 percent at very low spatial frequencies (wide spacing periods) and gradually drops with increasing spatial frequency. As spatial frequencies reach the Abbe limit (the imaging wavelength divided by twice the objective numerical aperture), contrast values are generally too low to detect individual spacings in the line grating.
In some instances, the modulation transfer function of an optical microscope can actually be less than zero. This occurs in an otherwise functional system when performance is degraded due to defocus, aberrations, and/or manufacturing errors. Often, the modulation transfer function will oscillate above and below zero as the microscope is racked through the point of best focus on a specimen having features with high spatial frequency. When the transfer function dips below zero, the image undergoes a phase reversal in which dark features become bright and vice versa.
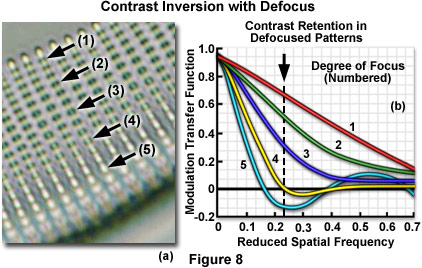
This phenomenon is illustrated in Figure 8(a) for the periodic knobs imaged from the curved surface of a diatom frustule. As the microscope focus is changed, the knobs undergo inversion of contrast, producing a ripple effect in the relative modulation (compare knobs (1) through (5) in Figure 8(a)). Increasing the degree of defocus will produce a corresponding increase in the oscillations observed with a modulation transfer function plot, with contrast reversals affecting increasingly larger features in the image. As the specimen plane is defocused, contrast drops rapidly for microscopic feature having high spatial frequencies and more slowly for those with low frequencies. It is often useful to measure contrast at a particular spatial frequency and then follow contrast as a function of distance on either side of the image plane. This analysis is sometimes termed the through-focus transfer function and is a measure of the depth of focus for a particular objective.
In figura 7(a) e' mostrata una tipica scansione di intensita' fatta a partire da un target a stella, misurato con un obiettivo apocromatico ad alta apertura numerica che opera in trasmissione di luce. I valori di intensita' sono stati mediati sulla dimensione parallela al reticolo di linee del target. Quando questi tipi di dati sono raccolti per una certa varieta' di obiettivi a varie aperture numeriche e graficate come percentuali di contrasto in funzione della frequenza spaziale, si ottiene un grafico simile a quello mostrato in figura 7(b). Il contrasto trasferito si avvicina al 100 % a bassisime frequenze spaziali (larghezza dei periodi spaziali) e gradualmente scende al crescere della frequenza spaziale. Quando le frequenze spaziali raggiungono il limite di Abbe ( la lunghezza d'onda divisa per il doppio dell' apertura numerica dell'obiettivo), i valori del contrasto sono generalmente troppo bassi per rivelare le singole spaziature tra le linee del reticolo.
In alcuni esempi, la modulation transfer function di un micrscopio ottico puo' benissimo essere minore di zero. Questo succede in un sistema altrimenti operante quando la prestazione e' diminuita per via del fuori fuoco, delle aberrazioni, e/o da errori di costruzione. Spesso, la modulation transfer function oscillera' sopra e sotto lo zero dal momento che il microscopio oscilla attraverso il punto di best focus su un campione ad alta frequenza spettrale. Quando la transfer function passa sotto lo zero, l'immagine subisce una inversione di fase in cui le caratteristiche scure diventano chiare e vice versa.
Il fenomeno e' illustrato in figura 8(a) per le protuberanze periodiche acquisite da una superficie curva della frustula di una diatomea. Quando il fuoco del microscopio viene cambiato, le protuberanze sono sottoposte ad una inversione di contrasto, che produce un effetto ripple nella relativa modulazione ( confronta le sporgenze(1) con le (5) in figura 8(a)). Aumentando il grado di defocus si produrra' un corrispondente aumento delle oscillazioni con un grafico della modulation transer function, con inversioni di contrasto che influiscono su caratteristiche sempre piu' grandi nell'immagine. Quando il piano del campione e' sfocato, il contrasto cade rapidamente per caratteristiche del microscopio aventi alte frequenze spettrali e piu' lentamente per quelle a basse frequenze. E' spesso utile misurare il contrasto per una particolare frequenza spettrale e seguire il contrasto in funzione della distanza sull'uno o l'altro lato del piano di immagine. Questa analisi e' a volte chiamata through-focus transfer function ed e' la misura della profondita' di fuoco per un particolare obiettivo.
The relationship between spatial frequency and the modulation transfer function for the diatom is illustrated in Figure 8(b). The graph represents a series of varying focus levels where the measured MTF is plotted against spatial frequency (number of sinusoidal features per unit distance). A drop in relative modulation values with defocus at fixed spatial frequencies is obvious in the figure, as well as the contrast reversal at focus levels 4 and 5 where the reduced spatial frequency drops into negative values of the MTF. Curve number 1 represents the diatom frustule in focus, and curves 2 through 5 present the results with successively increasing levels of defocus. The dotted line corresponds to the approximate spatial frequency of the knobs illustrated in Figure 8(a). Contrast is at a minimum where the dotted line crosses curve 4 and is reversed where curve 5 dips below zero on the y-axis.
All optical systems and supporting components including microscopes, digital and analog video systems, video capture boards, cables, computer monitors, photographic film emulsions, and the human eye each have a characteristic modulation transfer function. In the case of analog and digital electronic imaging detectors, the reciprocal relationship discussed above between spatial resolution and frequency response is valid. In this case, however, the point spread function is replaced by the time response to a very short electrical impulse, and the optical transfer function is replaced by the imaging system's response to the sinusoidal electrical signal with respect to amplitude and phase. Electronic systems lack the symmetry of optical systems, which introduces non-linear phase effects into the function. Regardless of these differences, the underlying concepts are similar between electronic and optical systems, and this allows optical microscopes coupled to digital (or analog) imaging equipment to be analyzed within a common framework.
The modulation transfer function of an optical system that contains a cascading series of components (microscope, digital video camera, video capture board, computer monitor, etc.) can be calculated by multiplying the individual MTF's of each component. By conducting a careful analysis of the combined system modulation transfer functions, a prediction about performance of the system can be obtained. In the same manner, the system phase response can be obtained by adding the phase transfer functions of individual components (Note: phase transfer functions are summed while modulation transfer functions are multiplied ). Together, the modulation and phase transfer functions define the optical transfer function of the system. It is important to point out that the contrast transfer function does not have the same mathematical properties as the modulation transfer function and cannot be obtained simply by multiplying the CTF of individual components.
In a cascaded series of devices that work together to produce an image, contrast is lost in certain frequency regions at each step, generally at the higher end of the spatial frequency range. In this regard, each detector or image processing function can also be used to cut off or boost the modulation transfer function at certain frequencies. At each stage, noise introduced by image transfer and processing is also a function of spatial frequency. Therefore, fine-tuning the response for optimum image contrast and system performance is dependent not only upon the type of image information desired, but also the frequency dependence of noise levels in the image. In addition, because the modulation transfer function of a detector is wavelength-dependent, it must be determined under carefully defined conditions of illumination.
The modulation transfer function has not yet been established for several contrast enhancing modes commonly utilized in optical microscopy (such as polarized light), which await more highly perfected theories of image formation and appropriate test patterns (or specimens) to determine, by experiment, the MTF values.
Authors
Kenneth R. Spring - Scientific Consultant, Lusby, Maryland, 20657.
Michael W. Davidson - National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., The Florida State University, Tallahassee, Florida, 32310.
In figura 8 (b) e' illustrata la relazione tra la frequenza spaziale e la modulation transer function per una diatomea. Il grafico rappresenta un serie di vari livelli di fuoco dove la MTF misurata e' graficata in funzione della frequenza spaziale (numero di oscillazioni sinusoidali per unita' di distanza). Nella figura e' evidente la caduta nei valori di modulazione relativi al defocus ad una frequenza spaziale fissata, come pure l'inversione di cotrasto ai livelli di fuoco 4 e 5 dove la ridotta frequenza spaziale cade verso valori negativi della MTF. La curva numero 1 rappresenta la frustula di una diatomea a fuoco, e le curve da 2 a 5 presentano i risultati di un succedersi di incrementi dei livelli di defocus. La linea tratteggiata corrisponde alla frequenza spaziale approssimata delle sporgenze illustrate in figura 8 (a). Il contrasto e' al minimo quando la linea punteggiata interseca la curva 4 ed subisce un'inversione dove la curva 5 inizia ad avere valori negativi sull'asse delle y.
Tutti i sistemi ottici e le componenti di supporto inclusi i microscopi, i sistemi video analogici e digitali, i video capture board, i collegamenti, i monitor dei computer, le emulsioni fotografiche delle pellicole, e l'occhio umano hanno una propria caratteristica modulation transfer function. La reciproca relazione tra risoluzione spaziale e risposta in frequenza, discussa sin ora, e' valida nel caso di rivelatori di immagini elettronici sia anologici che digitali. In questo caso tuttavia la point spread function e' sostituita dal tempo di risposta ad un impulso cortissimo, e la optical transfer function e' sostituita dalla risposta del sistema di imaging ad un segnale elettrico sinusoidale in riferimento all'ampiezza e alla fase. I sistemi elettronici sono privi della simmetria dei sistemi ottici, il che introduce effetti non lineari di fase nella funzione. Indipendentemente da queste differenze, i concetti di base tra sistemi elettronici ed ottici sono simili, e questo permette di accoppiare i microscopi ottici con sitemi di imaging digitali ( o analogici) da analizzare all'interno di una struttura comune.
La modulation transfer function di un sistema ottico che contiene una serie di componenti a cascata (microscopio, video camera digitale, video capture board, monitor del computer, etc.) puo' essere calcolata moltiplicando le singole MTF di ogni componente. Conducendo un'analisi attenta della modulation transfer function del sistema combinato, si puo' ottenere una valutazione delle prestazioni del sistema. Nella stessa maniera, la risposta in fase del sistema puo' essere ottenuta sommando le phase transfer function di ogni componente ( Nota: le phase transfer function sono sommate tra loro, invece le modulation transfer function sono moltiplicate). Insieme. la modulation e la transfer function definiscono la Optical transfer function del sistema. E' ' importante puntualizzare che la contrast transfer function non ha le stesse proprieta' matematiche della modulation transfer function e non puo' semplicemente essere ottenuta moltiplicando la CFT delle singole componenti.
In una serie di dispositivi in cascata che lavorano insieme per produrre un'immagine, si perde contrasto in alcune regioni di frequenze ad ogni passaggio, generalmente alla fine del piu' alto intervallo di frequenza spaziale. A questo proposito , ogni funzione di rivelazione o di image processing puo' essere usata per tagliare o aumentare la modulation transer function a certe frequenze. Ad ogni passaggio anche il rumore introdotto dall' aquisizione e dal processing della immagine e' funzione della frequenza spaziale. Quindi, il fine-tuning della risposta per un ottimo contrasto dell' immagine e la prestazione del sistema sono dipendenti non solo dal tipo di informazione sull' immagine desiderata, ma anche dalla dipendenza dalla frequenza dei livelli di rumore nell' immagine. In aggiunta, poiche' la modulation transfer function di un rivelatore e' dipendente dalla lunghezza d'onda, essa deve essere determinata attentamente in precise condizioni di illuminazione .
La modulation transfer function non e' ancora stata stabilita per molti diversi modi di miglioramento del contrasto comunenemente utilizzati nella microscopia ottica (come la luce polarizzata), che esigono teorie di formazione della immagine molto piu' elaborate e test pattern (o campioni) appropriati per determinare, sperimentalmente, i valori della MTF.
Authors
Kenneth R. Spring - Scientific Consultant, Lusby, Maryland, 20657.
Michael W. Davidson - National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., The Florida State University, Tallahassee, Florida, 32310.